【導讀】本文對變壓器空載時電路中的合閘電流進行了詳細的分析。通過公式分析的方式為大家講解了再變壓器空載合閘瞬間的變化,在掌握其中的的原理之后,即便再出現(xiàn)各種各樣的問題,相信大家也能經(jīng)過思考順利解決。
在變壓器設計過程中,偶爾會遇到變壓器空載的情況,其成為了困擾部分設計者的難題,想要解決變壓器空載問題,就首先需要全面的了解在空載合閘時的瞬變過程,在本篇文章當中,小編將對變壓器空載合閘電流瞬間的瞬變過程進行介紹。
在電路中,當在變壓器處于穩(wěn)態(tài)運行時,I0(空載電流)很小,大型變壓器甚至不到1%倍的額定電流;但在空載時,變壓器突然接入電網(wǎng),此瞬時可能有很大的沖擊電流,是空載電流的幾十倍到幾百倍。此現(xiàn)象的存在主要是由于飽合和剩磁的存在。
空載合閘電流分析
建立方程,設外施電壓按正弦規(guī)律變化,并求解。
=1.414Usin(ωt+α)=+ωdΦ/dt(1)
其中,α為外施電壓初相角;im為激磁(原邊)電流瞬時值。
L=ωΦ/i即=ωΦ/Lav(2)
由于電力變壓器電阻較小,實質(zhì)上的存在是瞬態(tài)過程衰減的重要因素。
(2)代入(1)得磁通方程:
sin(ωt+α)=ωΦ/Lav+ωdΦ/dt(3)
解得:
Φ=Φsin(ωt+α-90°)+CE(4)
其中,Φ為穩(wěn)態(tài)時的磁通幅值,C為積分常數(shù),E為的(-t/Lav)次方。(2)確定C。
設鐵芯無剩磁t=0,Φ=0,代入(4)式得C=Φcosα(5)
從而Φ=-Φcos(ωt+α)+(Φcosα)E(6)
討論
①在初相角α=0時接通電源,則Φ=-Φcosωt+Φ
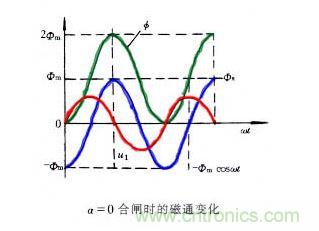
圖1
由圖1知,在合閘后的約半個周期,即當t=π/ω時,穩(wěn)態(tài)分量和瞬態(tài)分量的瞬時值相疊加,并考慮到剩磁,可達約Φ=2Φm,故此時磁路非常飽和,相應的激磁電流急劇增大可達正常時空載電流的幾百倍,額定電流的幾倍。
初相角α=π/2時接通電源,則:Φ=-Φsinωt(8)
說明變壓器即進入穩(wěn)態(tài),不含瞬變分量,是理想的合閘時間。一般小型變壓器電阻較大,電抗較小,衰減較快,約幾個周期可達穩(wěn)態(tài);大型變壓器,電阻較小,電抗較大,衰減較慢,可能延續(xù)幾秒鐘達穩(wěn)態(tài)。








